(一)RSA算法
属于非对称加密算法,由Ronald Rivest、Adi Shamir、Leonard Adleman在1977年公开发表。
(1)特点:公钥和私钥(存在数学关系)都可用于加密消息,用于加密消息的密钥与解密消息的密钥相反。
(2)公私钥关系:一个用于加密,另一个用于解密。从一个无法推导出另外一个。
(3)隐患:RSA 算法基于大数分解 (无法抵抗穷举攻击),量子计算对 RSA 算法构成较大威胁。拥有N量子位的量子计算机,每次可进行2N次运算,密钥为1024位的RSA算法,1台512量子比特位的量子计算机在1秒内破解。
(二)RSA应用
- SSH、OpenPGP、S/MIME和SSL/TLS都依赖于RSA进行加密和数字签名功能
- RSA在浏览器中使用,在不可信任的互联网中建立安全连接
- RSA签名验证是网络系统中的常见操作
(三)RSA算法
RSA(Rivest-Shamir-Adleman)算法是一种广泛使用的公钥加密算法。在RSA中,公钥和私钥是由一对大质数 p 和 q 生成的。公钥通常表示为 (e,n),私钥表示为 (d,n),
其中:
①n=p×q
②e 是公钥的指数,通常是一个小整数,且 1<e<ϕ(n) 且 e 与 ϕ(n) 互质。
③ϕ(n)=(p−1)(q−1) 是欧拉函数,用于计算 n 的卡迈克尔函数值。
④d 是私钥指数,满足 d×e≡1(modϕ(n))。
【读作:d 乘以 e 同余于 1 模 phi(n) 或者 d 乘以 e 的结果,在模 phi(n) 的意义下,等于1 】
注意:以上参数中,公钥(e,n)可以公开,其他参数不可以公开。
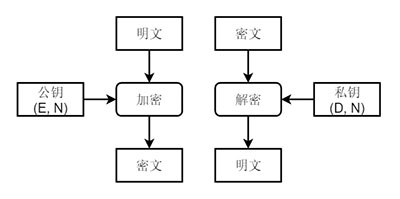
(1)加密
密文 = 明文E mod N
E和N的组合就是公钥(E, N)
(2)解密
明文 = 密文D mod N
D和N的组合就是私钥(D, N)
(3)生成密钥对
公钥是(E, N),私钥是(D, N),求E、D、N的过程就是生成密钥对的过程。
(四)RSA签名机制
RSA即可用于加密,也可用于签名。
签名公式(消息加密公式):签名=me mod n
(五)非对称加密算法
- 加密/解密
- 数字签名:发送方使用自己的私钥签署报文,接收方用对方公钥验证签名
- 密钥交换:通信双方协商会话密钥
(1)Elgamal算法
是基于迪菲-赫尔曼密钥交换的非对称加密算法,在1985年由塔希尔·盖莫尔提出。既能用于数据加密也能用于数字签名。是基于有限域中离散对数问题的难解性。
(2)DSA算法
DSA算法是 Schnorr 和 ElGamal 签名算法的变种,被美国 NIST 作为 DSS (Digital Signature Standard)。 基于整数有限域离散对数难题。
(3)DH(Diffie-Hellman)算法
又称密钥一致协议。由公开密钥密码体制奠基人Diffie和Hellman在1976年提出。原理是通过共享参数(公钥)、私有参数(私钥)及算法协商对称秘钥,然后用它加密后面的通信。
(4)ECC椭圆加密算法
由Koblitz和Miller于1985年提出。利用椭圆曲线上的有理点构成Abel加法群上椭圆离散对数的计算困难性。