树结构中的一个数据元素拥有≥2的直接后继元素,用来描述客观世界的层次关系。
(一)树的定义
树:是n(n>0)个结点的有限集合。
空树:当n=0时。
根结点:非空树有且仅有一个根结点。
子树(根结点外):根结点外的其他结点构成的互不相交的树。
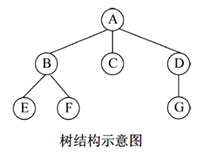
(二)相关概念
概念 | 描述 | |
1 | 双亲、孩子和兄弟 | 结点的子树的根为该结点的孩子,该结点称为其子结点的双亲。 具有相同双亲的结点互为兄弟。 |
2 | 结点的度 | 某结点的子树个数。 |
3 | 叶子结点 | 也称终端结点,指度为零的结点。 |
4 | 内部结点 | 度不为零的结点称为分支结点或非终端结点。 除根结点之外,分支结点也称为内部结点。 |
5 | 结点的层次 | 根为第一层,根的孩子为第二层,以此类推 |
6 | 树的高度(或深度) | 一棵树的最大层次数 求深度时,从上往下测量,求高度时,从下往上测量 |
7 | 有序(无序)树 | 将树中结点的各子树看成是从左到右具有次序的树 |
8 | 森林 | 互不相交的树的集合 |
(三)二叉树定义
(1)定义
是n个结点的有限集合。
①空树
②由一个根结点及两棵不相交的、分别称为左子树和右子树的二叉树所组成。
(2)树与二叉树
对比 | 子树 | 结点的度 | |
1 | 二叉树 | 区分左子树和右子树 | 最大度为2 |
2 | 树 | 不区分 | 不限制 |
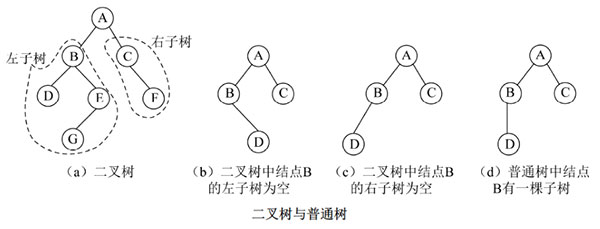
(四)二叉树性质
性质1:二叉树第i层 (i≥1)上至多有2i-1个结点
性质2:深度为k的二叉树至多有2k-1个结点(k≥1)
性质3:对任何一棵二叉树,若其终端结点数为n0,度为2的结点数为n2,则n0=n2+1
性质4:具有n个结点的完全二叉树的深度为「log2n」+ 1
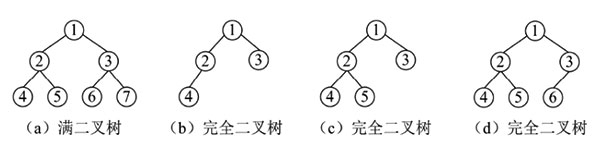
(1)满二叉树
除最后一层节点外,每个节点都有两个子节点,同时所有叶子节点都在最后一层。
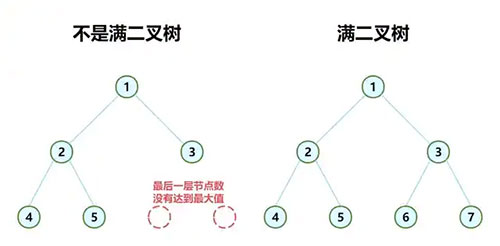
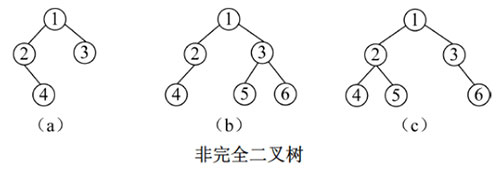
(2)完全二叉树
一棵树的叶子节点只能出现在最后两层,且最后一层的节点都集中在左侧且从左到右是连续的。
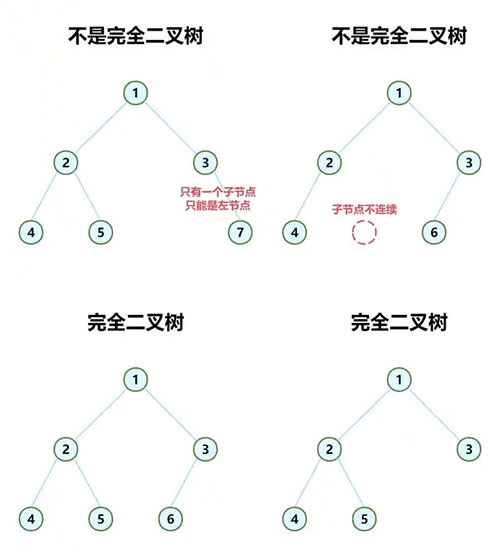
(五)二叉树存储结构
存储结构 | 说明 | |
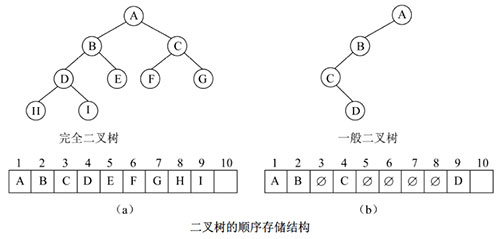
1 | 顺序存储结构 | 用一组地址连续的存储单元存储二叉树的结点(适当的线性序列),结点在序列中的相互位置能反映出结点之间的逻辑关系。 对完全二叉树而言既简单又省空间,不适用于一般二叉树(“虚结点”浪费空间)。 |
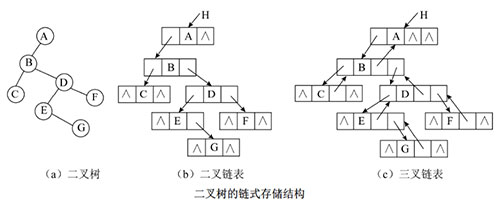
2 | 链式存储结构 | 用三叉链表或二叉链表来存储二叉树,链表头指针指向二叉树根结点。 |
(六)二叉树遍历
遍历:是按某种策略访问树的每个结点,且仅访问一次。
依据访问根结点位置的不同,分为前序、中序和后序三种遍历方法。
中序操作过程
(1)中序遍历根的左子树
(2)访问根结点
(3)中序遍历根的右子树
对含有n个结点的二叉树,遍历算法的时间复杂度都为O(n),栈的容量恰为树的高度。
在最坏情况下,二叉树是有n个结点且深度为n的单枝树,遍历算法的空间复杂度也为O(n)。
(七)最优二叉树
(1)最优二叉树
又称哈夫曼树,是一类带权路径长度(WPL)最短的树。
● 特点
1)每个初始结点最终都成为叶结点,且权值越小的结点到根结点的路径长度越大。
2)构造过程中共新建了n-1个结点 (双分支结点),因此结点总数为2n- 1 。
3)每次构造都选择2棵树作为新结点的孩子,因此不存在度为1的结点。
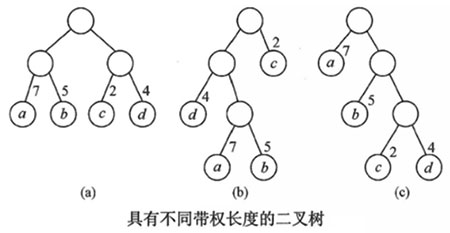
如图,c树的WPL=35最小,经验证其为哈夫曼树。
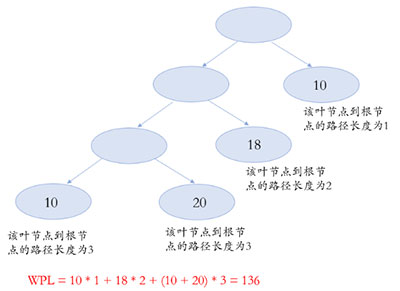
从树中一个结点到另一个结点之间的通路称为结点间的路径,该通路上分支数目称为路径长度。树的路径长度是从树根到每一个叶子之间的路径长度之和。
结点的带权路径长度:从该结点到树根之间的路径长度与该结点权的乘积。
树的带权路径长度:树中所有叶子结点的带权路径长度之和
(2)构造最优二叉树的哈夫曼方法
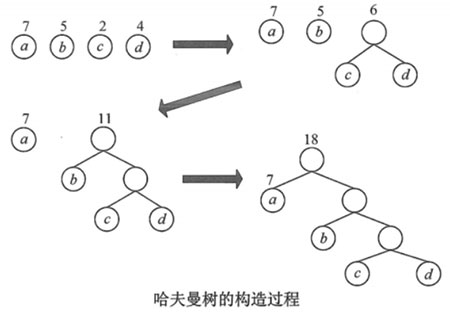
方法:每次从权重集合取出权重最小的两个节点,生成一个中间节点作为这两节点的父节点,再将父节点并入集合,直到完整的树构建完毕。
例如,权值{7, 5, 2, 4}的哈夫曼树的构造过程如图
最优二叉树的应用:对字符集中的字符进行编码和译码。
(八)二叉查找树
二叉查找树:又称二叉排序树,二叉搜索树,或者是一棵空树,或者是具有如下性质的二叉树。
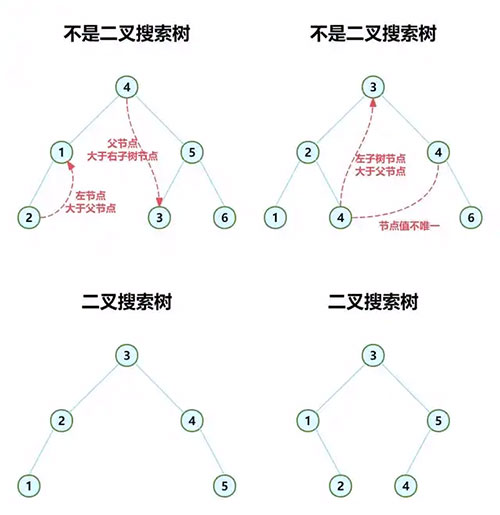
(1)若左子树非空,则左子树上所有结点的关键码值均小于根结点的关键码值;
(2)若右子树非空,则右子树上所有结点的关键码值均大于根结点的关键码值;
(3)左、右子树本身就是两棵二叉查找树。
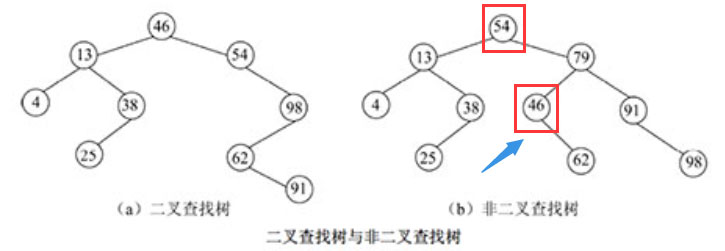
对二叉查找树进行中序遍历,得到一个关键码递增有序的结点序列。