矩阵是很多科学与工程计算问题中研究的数学对象。
在一些矩阵中,存在很多值相同的元素或者是零元素。为了节省存储空间,可进行压缩存储。
矩阵压缩存储:为多个值相同的元素只分配一个存储单元,对零元不分配存储单元。
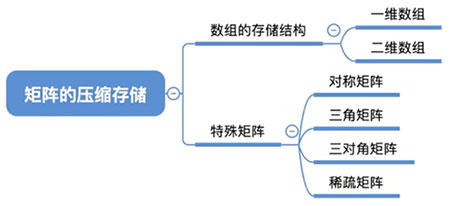
(一)特殊矩阵
特殊矩阵:对称矩阵、三角矩阵和对角矩阵。
对于特殊矩阵,由于其非零元分布都有一定规律,可将其压缩存储在一维数组中,并建立起每个非零元在矩阵中的位置与其在一维数组中的位置之间的对应关系。
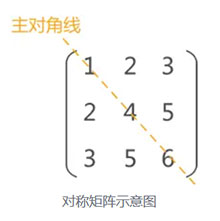
对角矩阵:指矩阵中的非零元素都集中在以主对角线为中心的带状区域中,即除了主对角线上和直接在对角线上、下方若干条对角线上的元素外,其余矩阵元素都为零。

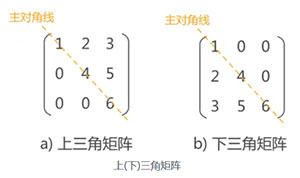
上下三角压缩存储方式:采用对称矩阵的方式存储,最后一位存储常量。
(二)稀疏矩阵
稀疏矩阵:在一个矩阵中,若非零元素个数远少于零元素个数,且非零元素的分布没有规律。
对于稀疏矩阵,存储非零元素时必须同时存储其位置(即行号和列号),三元组可唯一确定矩阵中的一个元素。
一个稀疏矩阵可由表示非零元素的三元组及其行、列数唯一确定。
三元组顺序表:由稀疏矩阵的三元组表构成的具有顺序存储结构的线性表。
十字链表:上述线性表改为链式存储结构。


存储的是三元组(即由 3 部分数据组成的集合),组中数据分别表示(行标,列标,元素值)