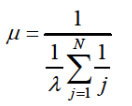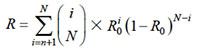(一)计算机可靠性概述
计算机系统硬件故障通常是由元器件的失效引起的。
(1)元器件可靠性
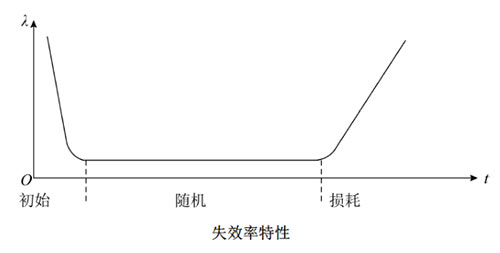
分成三个阶段(“浴盆曲线")
1)开始阶段器件工作处于不稳定期,失效率较高(老化筛选);
2)器件进入正常工作期,失效率最低,基本保持常数;
3)元器件开始老化,失效率又重新提高(淘汰)。
(2)计算机系统可靠性
指从开始运行(t=0)到某时刻t这段时间内能正常运行的概率,用R(t)表示。
失效率:指单位时间内失效元件数与元件总数的比例,用λ表示,当λ为常数时,
可靠性与失效率关系:R(t)=eλt
(3)失效率与时间关系曲线
(4)平均无故障时间(Mean Time Between Failure,MTBF)
两次故障之间系统能正常工作的时间的平均值:MTBF=1/λ
(5)平均修复时间(MTRF)
表示计算机的可维修性,即计算机的维修效率,指从故障发生到机器修复平均所需要的时间。
(6)计算机可用性
是指计算机的使用效率,以系统在执行任务的任意时刻能正常工作的概率A来表示,即:
A=MTBF/(MTBF + MTRF)
(7)计算机RAS
可靠性R(reliability)、可用性A(availability),可维修性S(Maintainability)
在实际应用中,引起计算机故障的原因除了元器件以外,还与组装工艺、逻辑设计等因素有关。
(二)计算机可靠性模型
(1)可靠性模型
可靠性模型 | 说明 | 可靠性R | 失效率λ | |
1 | 串联系统 | 某系统由N个子系统组成,当且仅当所有的子系统都能正常工作时,系统才能正常工作 | R=R1*R2*R3 | λ=λ1+λ2+λ3 |
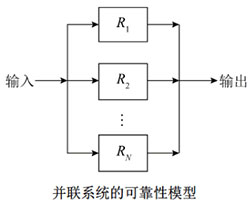
2 | 并联系统 | 某系统由N个子系统组成,只要有一个子系统正常工作,系统就能正常工作 随着冗余子系统数量增加,系统平均无故障时间也会增加 | R=1-(1-R1)*(1-R2)*(1-R3) |
|
3 | N模冗余系统 | 在N个(N=2n+1)子系统中,系统数≥n+1能正常工作,系统就能正常工作 |
|

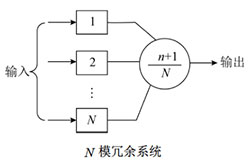
【例】设某系统由三个相同子系统构成,每个子系统的可靠性度量值为0.9,平均无故障时间(MTBF)为10000小时,求系统的可靠性和平均无故障时间。
分析:R1=R2=R3=0.9,失效率λ=λ1=λ2=λ3=1/10000=1x10-4
系统可靠性度量值:R=1-(1-R)3=0.999
系统平均无故障时间:
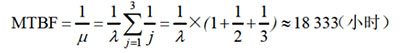
(2)提高可靠性的措施
①提高元器件质量,改进加工工艺与工艺结构,完善电路设计。
②发展容错技术,在计算机硬件存在故障的情况下,仍能继续运行,得出正确结果。