2.2.3 网络与最大流量

2026-02-04 17:32:38 更新

【选择计算题】最大流量问题是特殊的线性规划问题。

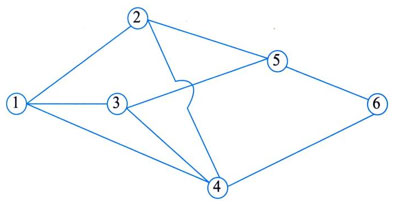
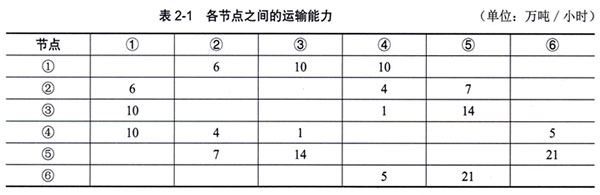
下图标出了某地区的运输网，以及各节点之间的运输能力。

● 流的要求：每条边（弧）上的流量不能超过该边的最大通过能力（即边的容量），中间节点的流量为0。

● 节点流量：对于每个节点，运出该节点的产品总量与运进该节点的产品总量之差，是其净输出量。

● 中间节点：只起到转运作用，流量为0。

● 方案总运输量：起始点的净流出量和终点的净流入量必须相等。

在本例中，从节点①到节点⑥可以同时沿多条路径运输，总的最大流量应是各条路径上的最大流量之和，每条路径上的最大流量应是其各段流量的最小值。

计算时，每找出一条路径算出流量后，该路径上各段线路上的流量应扣除已经算过的流量，形成剩余流量。剩余流量为0的线段应将其删除（断开）。

从节点①到节点⑥的最大流量应是所有可能运输路径上的最大流量之和，即10+6+5+1+1=23万吨。

按照习惯，每次应尽量先找出具有最大流量的路径。理论上可证明，总的最大流量是唯一确定的。