2.4.3 数学建模的基本方法

2026-02-01 05:46:01 更新

1）数学模型

是客观世界中的实际事物的一种数学简化，常以某种意义上接近实际事物的抽象形式存在，和真实事物有着本质区别。可以使用数学语言来描述数学模型。

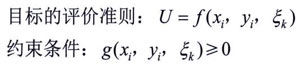
其中：x_i为可控变量，y_i为己知参数，ξ为随机因素。

● 目标的评价准则一般要求达到最佳（最小或最大）、适中、满意等。准则可以是单一的，也可以是多个的。约束条件可以没有，也可有多个。当g是等式时，即为平衡条件。

● 模型分类

	分类标准	模型
1	有无随机因素	确定性模型、随机模型（评价准则用期望值、方差或某种概率分布表示）
2	可控变量取值	离散模型、连续模型
3	按使用的数学工具	代数方程模型、微分方程模型、概率统计模型、逻辑模型等
4	用求解方法	直接最优化模型、数字模拟模型、启发式模型等
5	按用途	分配模型、运输模型、更新模型、排队模型、存贮模型等
6	用研究对象	能源模型、教育模型、军事对策模型、宏观经济模型等

2）数学建模过程（把复杂实际问题简化、抽象为合理的数学结构的过程）

	步骤	描述
1	模型准备	了解问题实际背景，明确其实际意义，掌握对象各种信息，用数学语言描述问题。在模型准备阶段要深入调查研究，虚心向实际工作者请教，尽量掌握第一手资料。
2	模型假设	根据实际对象的特征和建模的目的，对问题进行必要简化，并用精确的语言提出一些必要的、合理的、简化的假设。此举关系到建模的成败
3	模型建立	在假设基础上，利用适当的数学工具来刻画各变量之间的数学关系，建立相应的数学结构。只要能够把问题描述清楚，尽量使用简单的数学工具。
4	模型求解	利用获取的数据资料，对模型所有参数做出计算（估计）。可以采用解方程、画图形、优化方法等数学方法，特别是可以利用数学软件和计算机技术。
5	模型分析	对所得的结果进行数学上的分析。如结果的误差分析、统计分析、模型对数据的灵敏性分析、对假设的强健性分析等。
6	模型检验	将模型分析结果与实际情形比较，以此来验证模型的准确性、合理性和适用性。对于模型是否真的有用非常关键，要以严肃认真的态度对待。
7	模型应用	应用方式因问题的性质和建模的目的而异。

3）建模方法和思路

	方法	描述
1	直接分析法	根据对问题内在机理的认识，直接构造出模型
2	类比法	根据类似问题的模型构造新模型
3	数据分析法	通过试验，获得与问题密切相关的大量数据，用统计分析方法进行建模
4	构想法	对将来可能发生的情况给出逻辑上合理的设想和描述，然后用已有方法构造模型，并不断修正完善，直至比较满意为止。