● 确定性现象(必然现象):在一定条件下必然发生,可以事前预言,结果是确定的。
【例】自由落地运动,异性电荷相互吸引
● 随机现象:在一定条件下可能发生也可能不发生,在观察之前无法预知它的准确结果。
【例】抛硬币、股票价格、彩票号码
1)事件
(1)随机试验:可以在相同条件下重复进行,并且每次试验的结果事先不可预知。(抛硬币)
(2)随机事件(事件):在随机试验中,可能发生也可能不发生的事件。(骰子点数为奇数)
(3)样本点:随机试验中每一个可能的试验结果。
(4)样本空间:样本点的全体,常用Ω表示(读音Omega)。{正面,反面}、{1,2,3,4,5,6}
(5)必然事件:必然发生的事件,应包含所有样本点Ω。(骰子点数<7)
(6)不可能事件:不可能发生的事件。不包含任何样本点,记作∅(空集)。(骰子点数为8)
(7)子事件:如果事件A发生必然导致事件B发生,则称A是B的子事件,或称事件B包含事件A,记为A⊆B;如果A⊆B且B⊆A,则A与B同时发生或不发生,则称A等于B,记作A=B。
●事件分类
事件 | 描述 | 符号 | |
1 | 和(或、并)事件 | 事件A和事件B至少有一个发生 | A∪B(或A+B) |
2 | 积(与、交)事件 | 事件A和事件B同时发生 | A∩B(或AB、A*B) |
3 | 差事件 | 事件A发生且事件B不发生 | A-B |
4 | 互斥(互不相容)事件 | 事件A与事件B不可能同时发生 | A∩B=∅ |
5 | 逆(对立)事件 | 事件A与事件B有且只有1个发生 | A∪B=Ω且A∩B=∅ |
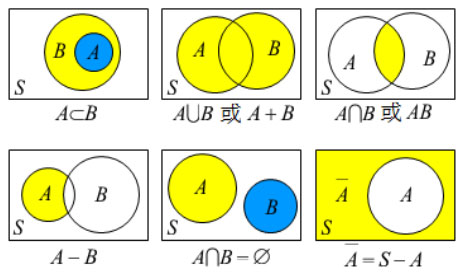
注意:逆事件一定是互斥事件,但互斥事件不一定互为逆事件
2)概率(选择题)
在不变的条件下,重复做n次试验,设n次试验中事件A发生m次。如果当n很大时,频率m/n稳定在数值p附近摆动,且随着n增大,摆动幅度变小,称数值P为事件A的概率,记作P(A) = p(probability)
●频率:(实际看到的)在有限次试验中,某一事件发生的次数占总试验次数的比例。
●概率:(相信的规律)在理想条件下,事件发生的长期稳定的可能性。
(1)概率基本性质
① P(∅) = 0 , P(Q) = 1。注意:概率为0的事件不一定是不可能事件,概率为1的事件不一定是必然事件
② 对于任何事件A,0≤P(A)≤1
③ P() = 1-P(A) (A的逆事件)
④ P(A-B) = P(A)-P(AB)
⑤ 当B⊆A时,则P(A-B) = P(A)-P(B)
(2)条件概率和事件独立性
如果A,B是两个事件,且P(A) > 0
为事件A发生的条件下事件B发生的条件概率
如果P(AB) = P(A)P(B),则称A与B相互独立。由此推出A与B相互独立当且仅当P(B|A) = P(B)。
即A与B相互独立意味着B发生的概率与A是否发生无关。同样,A发生概率与B是否发生也无关。
●条件概率:知道了更多信息,概率会发生更新
●事件独立性:两个事件独立,一件事发不发生,不影响另一件事发生的概率
(3)加法公式(任何2个或多个事件至少有1个发生)
① P(A∪B) = P(A) + P(B) - P(AB)
② P(A∪B∪C) = P(A) + P(B) + P(C) - P(AB) - P(AC) - P(BC) + P(ABC)
(4)乘法公式(由条件概率公式变化而来)
① 设P(A) > 0,则P(AB) = P(A)P(B|A)
② 设P(A1,A2…An-1)>0,则
(5)全概率公式(知道某些原因会导致该结果,求该结果可能性大小)
(6)贝叶斯(Bayes)公式(知道了该结果,求哪种原因可能性更大)
P(A|B):在B发生情况下,A发生的概率(后验概率,我们想求的)。
P(B|A):在A发生情况下,B发生的概率(似然,通常从数据或已知信息得到)。
P(A):A发生的概率(先验概率,在考虑新证据之前的信念)。
P(B):B 发生的总概率(证据的边际概率)。
(7)伯努利二项概率公式(二项概率公式)
● 伯努利概型:在相同条件下,将同一试验重复做n次(相互独立),每次试验结果只有两种可能。常用于生活中可用于任何重复的“是/否”随机试验的概率计算。
● 在伯努利概型中,如果事件A在每次试验中发生概率为p,则在n次试验中事件A恰好发生k(0≤k≤n)次的概率为